Numerical Modelling
Development of Numerical Models
The Chair has developed the pioneering numerical framework MultiFlow (http://www.multiflow.org) to predict the behaviour of single-phase and multiphase flows, including gas-solid, gas-liquid and particulate flows, at several scales of interest. The fluid solver consists of a fully-coupled pressure-velocity algorithm for any number of fluid phases and ranges from incompressible to compressible flow. In multi-phase flow problems, this enables the efficient, stable and accurate prediction of such flows in the Eulerian-Lagrangian, Eulerian-Eulerian, Volume-of-Fluid (VoF) and Immersed Boundary (IBM) frameworks.
Computational Fluid Dynamics
In our research on Computational fluid dynamics (CFD) we employ novel numerical methods to solve complex fluid flows. We have developed a so-called fully-coupled framework, in which the governing equations (e.g. the continuity, momentum, energy, etc.) are solved as part of a single system of coupled equations. This has been done for single phase and multiphase flows, laminar and turbulent. We also perform research across the scales; ranging from direct numerical simulation (DNS) and large eddy simulation (LES), to the transient Reynolds averaged Navier-Stokes (tRANS) framework.
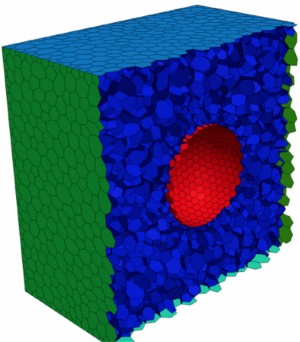
Complex Geometries
As most processes in Mechanical Process Engineering occur in complex geometries, the numerical algorithms are developed to function within arbitrary domains. The discretisation of the governing equations on unstructured meshes, such as tetrahedral or polyhedral meshes, involves additional difficulties compared to the discretisation on structured meshes, due to the additional topological complexity of unstructured meshes. The discretisation must account for geometric errors, such as mesh skewness and non-orthogonality, to provide a robust and accurate solution. Complex geometries are also taken into account when considering particulate flows or interfacial flows.