Dr. Sören Schenke

Institut für Verfahrenstechnik
Lehrstuhl Mechanische Verfahrenstechnik
About myself
Sören Schenke obtained his MSc degree in Naval Architecture and Ocean Engineering at Hamburg University of Technology. His Master thesis project at DNV GL Hamburg and the Institute for Fluid Dynamics and Ship Theory was on the further development and implementation of a numerical method to couple a RANS and a boundary element flow solver. He obtained his PhD degree at Delft University of Technology at the Department of Maritime and Transport Technology and at the Department of Process & Energy. His research was funded by the Marie Skłodowska-Curie ITN project CaFE and the MARIN Academy. The research was concerned with the development of a novel approach to compute cavitation implosion loads from energy balances in numerical flow simulations.
My project
Microbubbles play an important role in the field of diagnostic and therapeutic medical ultrasound treatment. The dynamic response of microbubbles exposed to focused ultrasound fields can be utilized for the treatment of vascular thrombosis and kidney stones, as well as for the non-invasive opening of the blood brain barrier or the enhancement of cell membrane permeability to aid targeted drug delivery. In high-intensity focused ultrasound fields, the nonlinear response of microbubbles leads to periodic inertial collapses and the emission of high-amplitude acoustic waves with significant subharmonic and ultraharmonic content. The thermo-viscous attenuation of higher wave harmonics is associated with strong local heat deposition in tissue. Therefore, a precise understanding of the acoustic wave dynamics and the capability to predict the behavior of nonlinear acoustic waves is crucial for the efficiency and the safety of focused ultrasound treatment. This research project consists of two parts. The first part involves the development of a numerical method to simulate nonlinear acoustic waves emitted from oscillating cavitation bubbles. The second part is concerned with the numerical simulation of the nonlinear interaction of acoustic waves in bubble populations in an existing Eulerian-Lagrangian framework.
Part I: Nonlinear acoustic wave dynamics
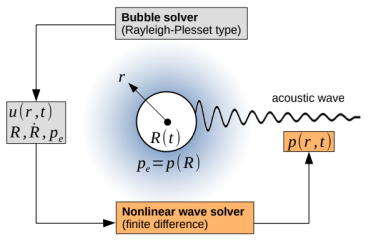
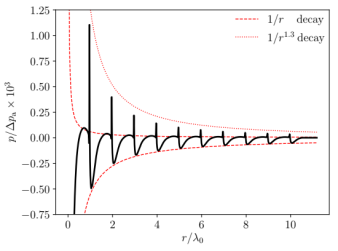
This part of the research project focuses on the numerical simulation of nonlinear acoustic waves in a moving medium and for moving wave emitting boundaries. This is the situation for an oscillating cavitation bubble as indicated in the schematic below (left). The time-dependent motion of the bubble wall displaces the surrounding fluid, in which the emitted acoustic waves propagate. Two solvers are coupled with each other in order to simulate the motion of the bubble wall (bubble solver) and the propagation of the emitted nonlinear pressure waves (wave solver) in spherical symmetry. The bubble solver provides the solution of different Rayleigh-Plesset type equations of motion of the bubble wall for a time-dependent ambient excitation pressure, and gives the kinematic parameters of the bubble wall motion (position and velocity), the radiated pressure perturbation, as well as the radial distribution of the fluid velocity. These quantities are treated as an input to the wave solver, which is based on the nonlinear Westervelt equation to account for the cumulative distortion of finite amplitude pressure waves due to the constitutive nonlinearity of the medium, as well as the thermo-viscous attenuation of the wave. A convective form of the equation accounts for the motion of the background medium as obtained from the bubble solver, and suitable coordinate transformations allow to account for the motion of the wave emitting bubble wall in a standard finite difference framework. The figure below (right) shows an example of a pressure wave profile emitted from a periodically collapsing bubble. It can be seen that the high-amplitude pressure peaks, emitted at the time instant of collapse, are attenuated at a higher rate than the linear wave parts.
 |
 |
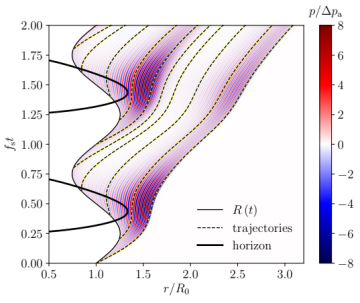
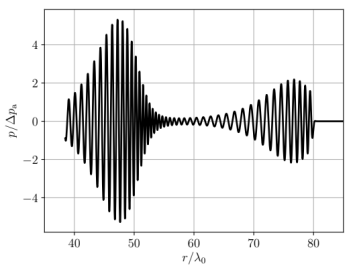
When an acoustic source moves at constant speed, a fixed observer perceives the well-known Doppler shift of the received wave frequency. If the source accelerates relative to a resting medium, nonlinear Doppler modulations occur, giving rise to frequency side-bands and amplitude modulations of the acoustic wave. The Leslie speaker is a prominent example in which this effect is utilized. The understanding of nonlinear Doppler effects can help to identify moving acoustic sources based on their acoustic signature. In a moving medium, the propagation speed of the wave relative to a fixed observer is altered as well. A point of transition from subsonic to supersonic flow speed in downstream direction forms an apparent sonic horizon as any wave in the supersonic region cannot pass that point. An example of both the aforementioned nonlinear Doppler modulations and the sonic horizon is shown in the figures below. A spherical wave emitting boundary oscillates in sinusoidal fashion and radiates acoustic waves at a frequency higher than the oscillation frequency. In the space-time diagram of the acoustic pressure, the sonic horizon is indicated by the black solid line. Outside the horizon, the trajectories of the acoustic perturbations evolve in positive radial direction, and inside the horizon, they evolve in negative direction. The numerical simulation of such situations is of potential interest to investigate the behavior of acoustic waves in black hole analogues.
 |
 |
Part II: Eulerian-Lagrangian modeling of bubble populations
While the first part of this research project focuses on the wave dynamics around an isolated acoustic source in spherical symmetry, the second part is concerned with the interaction of oscillating wave emitting cavitation bubbles. Based on the findings achieved in the research on isolated nonlinear wave dynamics, reduced models are derived for the propagation and interaction of acoustic waves in bubble clouds. The interaction model is incorporated in an existing numerical framework for Eulerian-Lagrangian methods. As a result, a more realistic representation of bubble cloud and acoustic wave dynamics under ultrasound excitation will be achieved.